Principe du risque d’un portefeuille d’actifs
La rentabilité d’un actif est une variable dépendant de son risque. La constitution d’un portefeuille d’actifs permet de se prémunir contre le risque. Par conséquent, plus l’on détient d’actifs différents, plus la diversification est optimale et le risque réduit. En effet, les différences en matière de rentabilité permettent de réduire le risque d’un actif spécifique. La baisse du cours d’une action (par exemple) pourra compenser la hausse du cours d’une autre.

Mesure de la rentabilité d’un portefeuille composé de deux actifs
Dans le cas d’un portefeuille composé de deux actifs, T1 et T2 avec une proportion de p1(T1) et de p2(T2), T1 et T2étant définis comme :
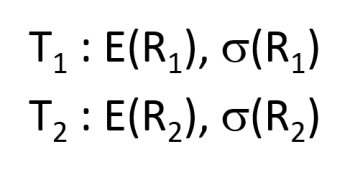
L’espérance de rentabilité du portefeuille sera de :
E(Rp) = p1 x E(R1) + p2 x E(R2)
Par exemple, si l’on a dans un portefeuille d’actifs deux actifs 1 et 2 avec une proportion de 30% de l’actif 1 et 70% de l’actif 2 et que ces actifs ont pour taux de rentabilité respectifs 12% et 7%, alors l’espérance de rentabilité du portefeuille d’actifs (soit le taux moyen de rentabilité du portefeuille) sera :
![]()
Le risque de l’actif 2 permet donc de contrebalancer le risque de l’actif 1 et de réduire l’exposition au risque de l’ensemble du portefeuille d’actifs.
Mesure du risque du portefeuille d’actifs
Absence de lien entre les rentabilités des actifs
Dans le cas où l’on observe pas de corrélation entre les variations des cours des actifs, les rentabilités des actifs sont indépendantes (un cours peut varier à la baisse et l’autre peut stagner par exemple). Dans ce cas, l’écart-type de la rentabilité est égal à la racine carrée de la variance de la rentabilité.
On a : V(Rp) : p1²V(R1) + p2²(R2)
Présence de corrélation entre les actifs du portefeuille
Si les deux rentabilités des deux actifs varient en même temps, ces deux actifs sont alors dépendants statistiquement. La formule de calcul du taux de rentabilité fait intervenir la covariance.
Soit Rp la rentabilité du portefeuille et b le taux de corrélation des actifs :
- Rentabilité lorsque les actifs varient dans le même sens dans des proportions identiques (corrélation = 1)

- Rentabilité lorsque les variations des actifs sont inversées (corrélation = -1)
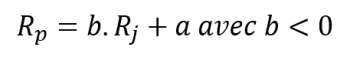
L’idéal pour la constitution d’un portefeuille est alors d’avoir une covariance négative pour minimiser le risque : la baisse d’un actif se compensera par la hausse de l’autre.


