La capitalisation est une notion clé en finance pour déterminer la rentabilité d’un investissement ou bien le coût d’un emprunt. Ce terme désigne la valeur d’une somme dans le futur placée au taux t% pendant n périodes. Grâce à la capitalisation, on peut estimer lesrevenus que l’on peut générer en plaçant son argent. Et ce, quelque soit le type de ces investissements : comptes d’épargne, obligations, actions, fonds communs deplacement…
Définition de la capitalisation
La capitalisation est un concept essentiel pour optimiser ses investissements. En comprenant comment elle fonctionne, on peut prendre des décisions de gestion éclairées. Et, par conséquent, maximiser ses rendements.
La capitalisation, c’est calculer la valeur acquise par une somme dans le futur, placée au taux t% pendant n périodes.
Autrement dit, la valeur acquise désigne ce que l’on a placé, augmenté des intérêts. C’est donc la somme totale que l’on récupère à l’issue du placement.
Calcul de la valeur acquise par un capital unique (C0)
Pour un capital unique (C0) placé au taux t% pendant n périodes, la formule de capitalisation est la suivante :
Au bout d’un an : C0 + C0xt% = C0(1+t%) = C1
Au bout de n périodes : Cn = C0(1+t)n
Avec :
-
- Cn : La valeur acquise (le montant total) après n périodes
- C0 : Le montant du capital initial
- t : Le taux d’intérêt périodique (exprimé en décimal)
- n : Le nombre de périodes
Par exemple, la valeur acquise (ce que l’on a placé augmenté des intérêts qui sont inclus dedans, c’est-à-dire la somme totale que l’on récupère à l’issue du placement) d’un placement de 15 000 € pendant une durée de 10 ans au taux nominal annuel de 4% est de :
C10 = 15 000 x (1+0,04)10
C10 = 22 203,66 €
Valeur acquise à la suite de n versements d’une somme a placée en fin de période au taux de i%
VA = a1(1+i)n-1 + a2(1+i)n-2 + a3(1+i)n-3 + … + an-1(1+i) + an
Cas particulier : Les sommes sont constantes : a1 = a2 = a3 = … = an.
On a alors : VA = a (1+i)n-1 + a(1+i)n-2 + a3(1+i)n-3 + … + an(1+i) + a, soit :
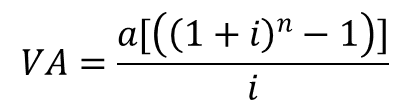
Exemple : On fait 10 versements sur un PEL (Plan d’Épargne Logement) en fin d’année de 10 000 € chacun. La rémunération est de 2,75%. Combien récupère-t-on après le dernier versement ?
On a donc :
VA = (10 000[((1+0,0275)^10-1)])/0,0275 = 113 327,65 €








